Spline

To create a spline, call the command Spline Creation:

Spline construction options both in the auto menu and in the Ribbon are combined into a separate group. You can open a group by clicking and holding  on the corresponding icon in the automenu. In the Ribbon, the group is expanded by pressing the image of the triangle to the right of the spline icon.

By default, a regular spline will be the first in the group. It is changed by one that was used last.

In the group of splines, there are three main types:

•Spline

•Spline by Polyline

•Polyline

Each of these types can be closed or non-closed.

Polylines are splines of the first order. Many parameters of points and additional parameters of splines are not available for them. Therefore, the description of the polylines is given after the subsection on the parameters of the splines.

To start creating a spline, you need to set the first characteristic point: it can be specified using , or you can specify its exact coordinates in the properties window.

To finish a spline creation press , <Ctrl + Enter> or complete the input using the window called by . The spline will be built to the last defined characteristic point.

If you press  once, the sequential input of characteristic points of the spline will be stopped and the spline will be in edit mode. You can resume entering points using and .

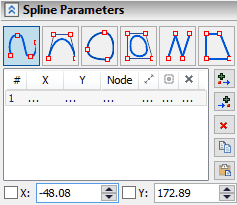
The type of the spline may be changed during the input process. To do this, click one of the icons in the properties window. After that, a spline of a different type is constructed along the entered characteristic points.

A spline of the first order can be constructed from two points; a spline of the second order can be built in three points; in order to construct a cubic spline, four points are necessary. When creating a spline, its order will automatically increase to the third. All splines by default are created as cubic. If you finish entering before defining the fourth point, a linear or quadratic spline will be created. The order of the spline is indicated in the properties window in the "Advanced" section. More information about the additional parameters of the spline will be discussed in the section "Spline parameters".

Spline

The spline is created by successively entering the coordinates of the characteristic points. The points can be specified using , or you can specify their exact coordinates in the properties window. If the coordinates are specified in the properties window, they should be confirmed by pressing <Enter> or pressing in the drawing field. The coordinates of the current point are located at the bottom of the spline parameters tab

.All the characteristic points are consequently displayed on tab of the spline parameters. Their coordinates can be changed. You can add points to the beginning or end of the spline, as well as to any desired place of the spline using the icons and .

If, for example, you need to add a new point between the second and third point, then you can select the coordinates of the second point using  and then click . After this, the current point will be the new point after the second. As before, its coordinates can be specified using  in the drawing field, or by entering exact values.

Both in the case of sequential input of points, and when additional points are entered, the change in the geometry of the spline will be dynamically displayed. Variants of the position of the new point will be determined by the position of the cursor. When specifying the characteristic points of the spline, all the usual bindings indicated in the bindings panel are available. Adding points with the help of and icons, both at the beginning or end of the spline, and in the specified area, the creation of the next new point will be proposed automatically. You can finish inputting new points the same way as completing the input of the spline.

Extra spline points can be deleted using . The coordinates of the selected point can be copied using . The copied coordinates can be passed into another point using .

New spline points can be added in the spline editing mode. To do this, just hover cursor over the spline and a dynamic image of a point moving along the spline and following the cursor will appear under the cursor. You should to specify the position of the point on the spline using .

Spline by Polyline

The principle of input of this spline is similar to the input of the usual spline Spline, where you should consequently specify the characteristic points. However, the Spline by Polyline does not pass through the characteristic points. In this type of spline, characteristic points define a polyline along which the spline is constructed.

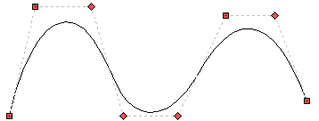
A polyline that defines a spline is indicated by a thin dashed line when creating or editing a spline. The image of characteristic points - as in other lines of a drawing. The position of the current characteristic point coincides with the cursor. The geometry of the spline is changed dynamically according to the position of the point.

The influence of each characteristic point on the spline is determined by the Weight parameter. The point can be suppressed - then the spline will be rearranged in the same way as if the point was removed.

Closed Spline

A closed spline passing through nodes is constructed using the option:

The principle of a closed spline creation does not differ from the standard spline creation. It is necessary to consistently create characteristic points that will determine the form of a closed curve. The dynamic image of the spline will appear only after entering the coordinates of the second point, since a closed curve can be created at a minimum of three points: Two of the points will be already set by the time the spline is displayed, and the position of the third will correspond to the position of the cursor.

Entering new points on a closed curve will occur in the area between the last and the first characteristic point. If you need to add points in other areas, you can do this by clicking . Then you should select a point, before which or after which you want to add a new point in the properties window. Then use the icon or .

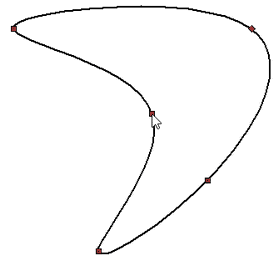
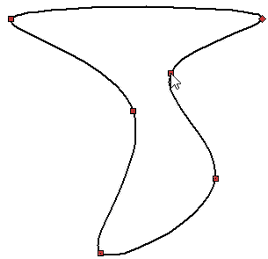
Closed Spline by Polyline

The principle of entering the characteristic points of a closed spline along a polyline is similar to the principle in the Closed Spline option. As in the Spline by Polyline option, characteristic points define the polyline along which the spline is created, and for each point there is an additional parameter Weight.

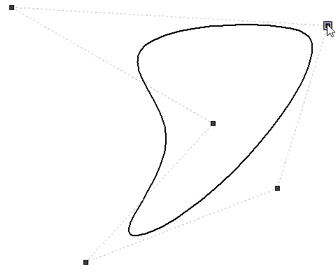
Spline Points Parameters

The parameters of the characteristic points of the normal spline and spline by polyline are different. Only one weight parameter (this parameter has already been described) and the ability to suppress the point are available for the characteristic points of a spline by polyline. As it was already mentioned, if you suppress a point, then it does not affect the creation of the spline, in the same way as if you delete it. The advantage of the Suppress option is that it can be set via a variable.

The parameters of characteristic points of options Spline and Closed spline provide great opportunities in the settings of the mathematical description of the spline.

It is possible to set the following parameters of the point:

•The length of the first derivative (the length of the tangent vector);

•Vector Angle;

•Radius of Curvature;

•Accuracy;

•Suppress Point.

The length of the tangent vector can be set exactly in the properties window, and an approximate value can be set using the manipulator. By default, the length of the tangent vector is given in mm, but the units of measurement can be changed. To do this, click  on the icon  of units.

The manipulator does not show the real length of the tangent vector, because the arrows of the manipulator are adapted to the current scale for convenience. Similarly, you can set the angle of the tangent vector: both with the help of the manipulator and in the properties window. The units of measurement can be changed (by clicking the icon  in the angle input field). By default the angle is measured in degrees [°].

The radius of curvature is specified in the same units as the length of the tangent vector. This is because the radius of curvature is a quantity depending on the functions of the spline and its derivatives. Therefore, if the units of measurement are changed in the field of values of the length of the tangent vector, then they will also change in the field of curvature radius. The symbol of the radius of curvature determines the direction of twisting of the spline: “-” sign will be clockwise, “+” sign will be against clockwise.

If the length of the tangent vector, the angle or radius of curvature were changed relative to those parameters that were calculated automatically, a flag is placed next to them and the value will be applied. If the flag is removed, the default value will be calculated.

The accuracy sets the maximum possible deviation of the spline from the points defining it. By default, the accuracy value is in mm, but, as is the case with the vector length, the units of measurement may be changed.

In order for an accuracy to be assigned for the selected point, you should enable the flag next to the field. If the accuracy flag is not active, the spline will pass through the point.

If the accuracy is not set, then the system of linear equations is solved for the spline with respect to the specified characteristic points. If you specify tolerance, then the problem with inequality is solved, taking into account the maximum possible given deviation.

Accuracy can be set to those points for which it is necessary, but the accuracy value for all selected points will be the same. If you change the value of the tolerance at one point - it will automatically change for all other points.

For example, for the 2 point of the spline, the accuracy is not active, and for the 3 and 4 it is active (for 1, 5 and 6 points, the tolerance parameter is not active).

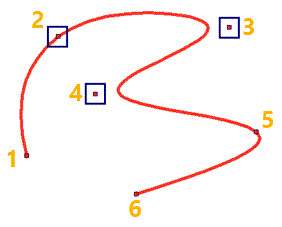
The Suppress option influences the geometry of the spline as if the point was deleted, but if you disable the Suppress flag, the point will again determine the geometry of the spline.

If changes were made in the point parameters, it will be shown in the spline properties window.

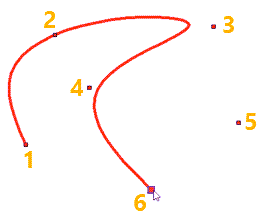
For point number 1 - no additional parameters are specified.

For point number 2 - a fixed value of the radius of curvature is set, if the vector angle of slope or length of the tangent vector were set, the same icon will appear.

For points number 3 and number 4 accuracy is set.

Point number 5 is suppressed.

Point number 6 is bind to the node (you can bind both to the point of a sketch and to the node on a construction line).

Spline Parameters

Unlike the parameters of points, the general parameters of the spline are the same for both normal splines and polylines. The following spline parameters are available:

•Spline degree;

•Type of parameterization.

For non-closed splines:

•Start extension;

•End extension.

Spline degree determines the degree of polynomials that describe the spline: polynomials of the first, second, third or fourth degree. By default, splines are built on cubic polynomials. If you specify the degree of the spline equal to one - the spline becomes a polyline.

The parameterization significantly affects the shape of the spline, especially in areas with closely spaced points that change the direction of the curve.

When changing the type of parameterization, the same parameter value may correspond to a different position on the spline. There will be a different length of the “arc” between two characteristic points of a spline.  

The following options for spline parameterization are available:

•By length,

•Centripetal,

•Uniform,

•Local sums,

•Fixed,

By default the Centripetal parameterization is used for splines.

Uniform. The characteristic points Dk, where k = 0,1, ..., n, are set for creation of a spline. The definition domain of the parameters is t [0,1]. The extreme parameters t0 = 0 and t1 = 1. Other parameters 1 / n, 2 / n, ..., (n-1) / n.

With uniform parameterization sharp protuberances, peaks, loops are possible more often than in other methods. At the same time, this type of parameterization is the most simple and intuitive.

By length. Parameters are distributed in accordance with the length of the arcs between adjacent points. The arcs between the points are curves constructed on polynomials, i.e. the spline can be represented as a sequence of such arcs.  

The characteristic points Dk, where k = 0,1, ..., n, are set for creation of a spline.

The length of all arcs (spline length) L will be determined by the expression:

Arc length Lk from D0 to Dk:
The definition domain of the parameters is t [0,1]. Each tk parameter should match the length Lk, then:  

t0=0 ,where k=0,1,…,n-1

t1=1

The arc length parameterization method is widespread and usually works well. You should take into account that the polynomial spline between two points is not an arc — it can be considered an arc only approximately. If the arc is long, a spline constructed using this type of parameterization can have a great convex.

Centripetal. The name of the method reflects its physical interpretation. When moving along a spline trajectory - the stronger the bend, the greater the centripetal force. The centripetal force is proportional to the angle change. The centripetal parameterization method is an approximation to such a physical model. From the point of view of mathematics, the centripetal method of parameterization is a modification of the method of parameterization by length.

The characteristic points Dk, where k = 0,1, ..., n, are set for creation of a spline. The definition domain of the parameters is t [0,1]. We introduce the exponent α, which will modify the expressions of the method of parameterization by length:

t0=0 ,where k=0,1,…,n-1

t1=1

If α = 1, then the centripetal parameterization and parameterization along the length give the same creation result.

If α˂1  and , then the influence of a longer arc decreases. Influence means the value of the parameter change for the corresponding arc.

If α<1  and , then the influence of a short arc increases.

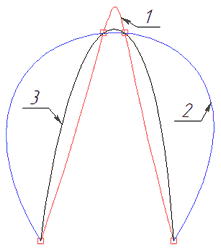
1 - Uniform parameterization, 2 - Arc parameterization, 3 - Centripetal parameterization

Local sums

This parameterization method is available for compatibility of splines built in T-FLEX CAD 15 and earlier. When creating splines in T-FLEX CAD 16 it is better to use the three listed above methods.

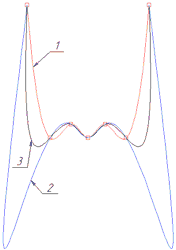
Fixed. When changing the position of characteristic points or adding points, the parameterization of the spline is recalculated. This is necessary when creating or editing a new spline, therefore, for the spline being built or being edited, the option of fixing the parameterization is disabled. If the spline was split (Split), or trimmed (Trimming) or imported from another system, then it will have a fixed parameterization. In the fixed parameterization mode, spline editing is limited. This is due to the fact that the length of the arc changes upon editing but the parameters values are fixed. When distance between points increases, flat areas can be formed, and when it decreases, loops are formed.

When trimming or splitting a spline, its parameterization type automatically becomes fixed. The type of parameterization for a fixed spline can be changed, but then its geometry will change. In the fixed parameterization mode, it is permissible to make only minor adjustments to the spline.

If the spline is built on three or two points  after editing, then changing the parameterization from fixed to any other is not recommended. By default, splines are built on the basis of cubic polynomials, and three points for the correct construction of a cubic spline are not enough. It is necessary either to lower the degree of the spline, or not to change the type of parameterization.

If the spline was split (Split), or trimmed (Trimming), then to save the geometry, the first and second derivatives are fixed at the two extreme points of the spline. If spline editing is necessary, it is recommended to remove the fixation of derivatives.

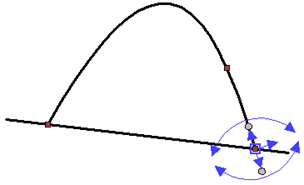
Offset allows you to lengthen the spline, or shorten (if you set a negative offset value). If the spline is lengthened, then it is necessary to choose the law of creation of the elongated part of the spline. For this, there are special options in the properties menu that will become available if you set a flag to activate the Start extension and/or End extension.

Let us consider the offset options.

Control determines how to set the length of the offset section. If the option By length is selected, then the length is set by the value in the selected units of measurement. If the option By parameter is selected, then the length of the extension region is specified in relative values. The influence of the parameter value on the length of the extension region depends on the type of parameterization of the spline.  Negative length and parameter values will shorten the spline.

Method of extension determines the law of the construction of the offset region. For negative offsets, the method of elongation does not affect the geometry of the spline.

The following extension methods are available.

•By straight line. With this method, only the first derivative is a smooth function. At the point of the beginning (end) of the spline, a tangent is constructed. Along the tangent, the displacement is calculated. Curvature is not preserved.

•Keep curvature. Both the first and second derivatives are smooth functions. This automatically sets a smooth decrease in curvature to zero. The offset section becomes straight with preservation of curvature.

•Mirror. The spline is reflected symmetrically relative to the line perpendicular to the tangent built at the point of the beginning (end) of the spline.

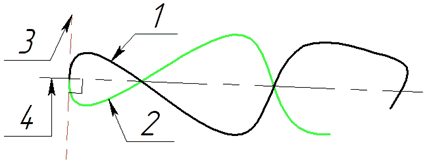
1 - source spline; 2 - extension section; 3 - tangent at the point of origin; 4 - perpendicular to the tangent

•By parameter. The curvature is preserved; a smooth decrease of the curvature occurs throughout the entire offset section. If the length of the offset section in the selected parameterization method reaches unity, then the curvature is zero and the radius of curvature is infinitely large.

•By arc. Only the first derivative is a smooth function, the curvature is not preserved. A tangent arc of a circle is constructed from the point of the beginning (end) of the spline, whose radius is equal to the radius of curvature at the point of the beginning (end) of the spline.  

Smoothness of splines at extreme points

If the extreme point of the spline coincides with the extreme point of another spline or line, then you can specify one of three options for the smoothness of the spline at the point of its transition to another line. The smoothness options are available in the pop-up menu when selecting the extreme point of the spline (provided that the extreme point coincides with the extreme point of another line), as well as in the automenu.

Smooth variations are denoted as G1, G2, G3.

<Shift + 1> G1 - the directions of the tangents coincide in the extreme points of the lines. This means that the angles of the first derivative of the lines at the extreme points will either be equal or differ by a multiple of 180°. For example, let's build two consecutive splines: the last point of the first spline coincides with the first point of the second. For the second spline at the first point, choose the smoothness G1. Now compare the angles of the tangent at the last point of the first spline and the first point of the second. The figure shows that they are equal.

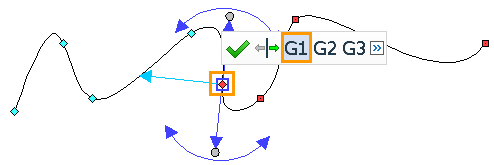
It should be noted that other parameters of the extreme points when using the smoothness of the G1 are different.

The use of G1 smoothness is possible only for splines of the second order and higher.

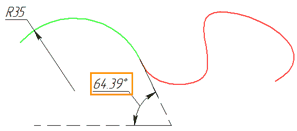
<Shift + 2> G2 - in the extreme points of the lines the directions of the tangents coincide and the centers of curvature coincide. This means that the equality of the radii of curvature at the extreme points of the curves is added to the condition G1. For example, build an arc with a radius of 35 mm from which is continued by a spline. We indicate the G2 smoothness at the first point of the spline. Now let's look at the radius of curvature at the first point of the spline. It can be seen from the figure that it is equal to 35 mm.

It should be noted that the sign of the radius of curvature reflects the direction of twisting of the spline (this was mentioned above). In addition, if you construct a tangent at the extreme point of the arc, then you can make sure that its direction will coincide with the direction of the tangent of the spline, since the angle of the constructed tangent is equal to the angle of the first derivative at the first point of the spline.

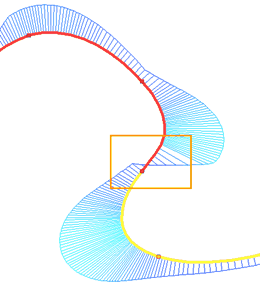
In the case when the spline and the curve to which the extreme point belongs have different twisting directions, the point of sign change (inflection point in the case of continuity) of the curvature function is at the extreme point of the spline. When using G2 smoothness, the inflection point will shift inside the spline, and a bend will be added to the spline itself with the same direction of twist as the curve to which the extreme point belongs. This is necessary to satisfy the condition of coincidence of the centers of the circles of curvature of the lines at the extreme points. Let's give an example. Let two consecutive splines be given. The last section of the first spline is twisted clockwise, the first section of the second is twisted in the opposite direction. We derive the curvature for these splines using the Show Curvature command (this command will be discussed in more detail in the next subsection).

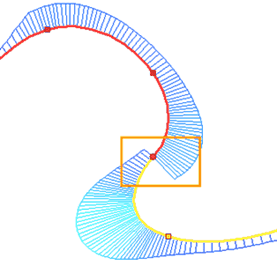
It can be seen from the figure that the curvature function changes sign at the last point of the first spline and the first point of the second spline, and in this case with the function breaking.

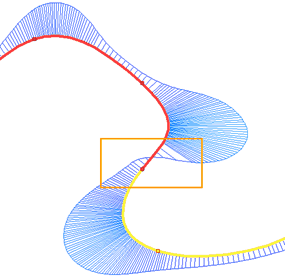
Apply the smoothness of G2 to the last point of the first spline. It can be seen from the figure that the inflection point has shifted into the first spline: a small section was added to the first spline with a twisting direction corresponding to the direction of the second spline.

It should be noted that the curvature function became continuous, but at the extreme points the smoothness of the curvature function is broken. To maintain the smoothness of the curvature function at the extreme points of the spline, there is a third version of smoothness.

The use of G2 smoothness is possible only for splines of the third degree and higher.

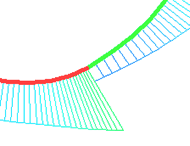
<Shift + 3> G3 - in the extreme points of the lines the directions of the tangents coincide, the curvature centers coincide and the directions of the tangents to the curvature function coincide. This means that the condition for the smoothness of the curvature function is added to the conditions G1 and G2. We continue the previous example with two consecutive splines. For the extreme point of the first spline, instead of the smoothness of G2, we choose the smoothness of G3. It can be seen from the figure that when using G3 smoothness, the curvature function preserves smoothness at the extreme points of the splines.

The use of G3 smoothness is possible only for splines of the fourth degree and higher. If the spline has a lower order than the fourth, then when you select the smoothness of the G3, the degree of the spline will be automatically increased to the fourth.

If we consider the smoothness of G1, G2, G3 from the point of view of their influence on the curvature function, then we can formulate the following rule:

G1 - the curvature function does not preserve continuity at the extreme points;

G2 - the curvature function is continuous, but does not preserve smoothness at the extreme points;

G3 - the curvature function is continuous and retains smoothness at the extreme points.

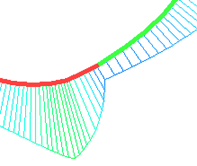
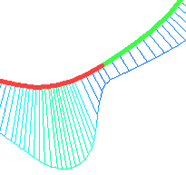
G1                                        G2                                        G3

A variant of the smoothness of the extreme points can be seen in the properties window of the spline.

The tangent angle at the extreme point can be changed by 180°. For this, in the pop-up menu and automenu of the extreme points of the spline, in addition to the options for smoothness, there is also the command <Shift + 4> Reverse Tangent Direction.

Spline Analysis

For the analysis of the geometry of the splines, there are two main tools: curvature of curves and radius of curvature. Curvature - the reciprocal of the radius of curvature. Curvature allows you to check the smoothness of the spline: preservation of curvature (smoothness of the second derivative).

Call the command to measure the curvature through the context menu. The context menu is invoked by clicking  on the spline. Then click  on the icon and call the Show Curvature command. This command can also be invoked via a Ribbon or text menu.

If the option is not called through the context menu, then you need to select the spline by clicking .

In the Show curvature option, you can change the displayed value from curvature to radius of curvature by activating the corresponding switch. The graphic output of the radius of curvature will be in millimeters.

The graphic output of curvature will be determined by the formula:

In the properties window, for convenience of curvature analysis, you can change the scale. The radius of curvature is always graphically displayed in real scale.

It is possible to show points with maximum curvature and points of bends: To do this, you need to set the appropriate flags in the properties window.

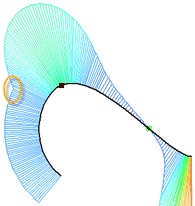
Curvature measurement helps to understand the difference in the law of construction of offsets for a spline. Some of them allow to preserve the smoothness of the second derivative (curvature), some - only the first (tangent).

The arc offset is the first derivative of a smooth function, the second (curvature) has a break.

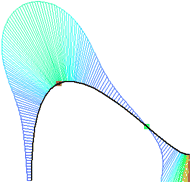
Parameter offset - curvature without kinks, a smooth decrease in curvature.

The Show Curvature command has the option to measure curvature values at any point.

When you call this option on the spline (as on any other line), a dynamically moving point will appear. Clicking  at the point under the cursor will measure the curvature and radius of curvature. The radius of curvature will be in meters, the curvature is the reciprocal of the radius of curvature in meters.

Polylines

As mentioned above, the polyline is a spline of the first degree. The principle of constructing, editing and adding new points is similar to the spline. For polylines, there are no additional spline parameters and no point parameters. Point can only be suppressed.  

Visually, when creating a polyline, we get consecutive segments. However, the interrelations of these segments is different than if we would draw segments in a coherent sketching mode or parametric segments (with constraint). In contrast to the specified options, a broken polyline is a single object.

For example, parts of a polyline cannot be rounded together, and when a segment is deleted, the deleted part will consist of a set of segments. You can create an offset curve to the polyline.